هناك مجموعة من النظريات الكونية البديلة Les Theacute;ories alternatives التي ظهرت في العقد الأخير من القرن العشرين المنصرم وفي العقدين الأولين من القرن الواحد والعشرين بعد سيادة وطغيان نظرية الانفجار العظيم أو الكبير Big Bang المعيارية كمسلمة في مجال الكوزمولوجيا أو علم الكون، والتي سنستعرض بعضاً منها باختصار شديد مع اعتذاري من القاريء الكريم لانسياقي رغماً عني في معمعمة المعادلات الرياضية والرسوم البيانية التي كان لا بد منها لشرح بعض المفاهيم وتقريبها لذهن القاريء قدر الإمكان مع معرفتي بنفور القراء من المعادلات الرياضيات في المقالات العلمية التبسيطية، والغرض من ذلك تنبيه القاريء وإيقاظ وعيه على معلومات ربما لم يكن على معرفة مسبقة بها تتعلق بنشأة الكون وهيكيليته وشكله وهندسته أو معماريته التي ظهرت كبديل للمعلومات والنصوص الدينية الثيولوجية التي تناولت هذا الموضوع من زاوية غيبية ماورائية..
نظرية جاك سارفاتي La theacute;orie de jack Sarfatti
جاك سارفاتي jack Sarfatti أستاذ جامعي يدرس في جامعة كاليفورنيا ويشرف على مجموعة بحث الفيزياء والوعي بغية إنعاش بحوث الفيزياء في هذه المجموعة. وملخص فكرته هي أن نظرية الكم الثقالية theacute;orie quantique de la gravitation تتطلب امتدادا لميكانيكا الكم يأخذ في الاعتبار الحالة النفسية للباحث أو المراقب!
إن هذه الفكرة أقل جنوناً عما تبدو عليه، وتستند على ملحقات وتوسعات لميكانيكا الكم مفصلة وشديدة التعقيد ومتخمة بالحسابات والمعادلات الرياضية الصعبة والتوريات اللغوية.
الفكرة الأساسية لنظريته تكمن في تحليل مفصل لما يسميه فاينمان Feynmann quot;السرأو اللغز الرئيسي لميكانيكا الكم principal mystegrave;re de la meacute;canique quantique quot;، عبر تجربة شق يونغ الشهيرة expeacute;rience des fentes d'Young حيث يلاحظ المرء الجسيمات الحبيبية granulaires تسلك سلوك الموجة ondulatoire. وعلى وجه الدقة، يحلل جاك سارفاتي ما يحدث عندما quot; يربط تخفيض حزمة موجة quot; بين نقطتين بعيدتين الواحدة عن الأخرى في الزمان والمكان وفي سرعة لا نهائية. وعند رصد لظاهرة معروفة في الفيزياء (وهي مرور الإلكترونات من خلال واحد من مكانين أو ثقبين) فإنه يتم تقليل وظيفة أو دالة موجة إلى الصفر فورا في كل مكان من الفضاء. وهذا تناقض كما تقول مجموعة الـ EPR الثلاثية حين تم تحليل هذا التناقض لأول مرة من قبل آينشتاين Einstein، و بودوفسكي Podowsky وروزين Rosen. إن تحليل الـ EPR وهي الحروف الأولى من أسماء الثلاثي المذكور أعلاه يظهر أنه على الرغم من التغيير الذي طرأ على وظيفة أو دالة الموجة بشكل فوري على نحو فعال في جميع أنحاء الفضاء، فإنه ليس من الممكن استخدامها لإرسال إشارة ذات معنى.
ووفقا لجاك سارفاتي، فإن الحد من حزمة موجة هو حالة محدودة ناجمة عن التقلبات الكوانتية fluctuations quantiques، ولكن من الممكن تحقيق انخفاض quot; خارج التوازنquot;، من شأنه في حد ذاته أن يمكننا أن نرسل إشارة بأسرع من الضوء. الفكرة الرئيسية هي ان يكون هناك حقل يسمى quot;الموجة التجريبية بوم onde pilote de Bohm quot; وهو الحقل أو المجال الذي يدفع أو يقود هذا التخفيض: إن هذه الموجة الموجهة هي التي تحدد quot;مشهد تجاذبات كسرية paysage d'attracteurs fractals quot; الذي يمكن تصوره على هيئة سطح صلب مليء بالحفر والمرتفعات، وبالتالي فإن الحد من وظيفة أو دالة موجة يتوافق مع سقوط كرة تقع في واحدة من التجويفات على هذا السطح. الكرة تمثل أحد الأكوان الموازية في تفسير مفهوم quot;العوالم المتعددةquot; (هوغ ايفرت الثالث hugh Everett III) لميكانيكا الكم meacute;canique quantique. الكرة تمثل هنا في هذا المثال كوننا (فضاء المراحل l'espace des phases) وهو يخضع للتقلبات الكمومية fluctuations quantiques، وكلما ظلت شدة كثافة الموجة الموجهة منخفضة إزاء هذه التقلبات، فإن اللاتماسك و اللاتناسق deacute;coheacute;rence،حيث يحدث الحد من وظيفة أو دالة الموجة، سيتم على ما يبدو على نحو عشوائي أو مصادفة aleacute;atoire ou par Hazard.
ومع ذلك فمن الممكن القول أن توليد ظروف تكون فيها الموجة القائدة أو الموجهة أكثر أهمية من هذه التقلبات الكوانتية: وفي هذه الحالة، فإن اللاتماسك و اللاتناسق deacute;coheacute;rence يتوافق مع المرحلة الانتقالية التي تمر بمرحلة انتقالية مشابهة لنظرية quot;الكم الكلاسيكيةquot; التي تم تحليلها باعتبارها نظرية الفوضى theacute;orie du Chaos: فالوضع اللامتماسك واللامتناسق العشوائي quot; deacute;coheacute;rence aleacute;atoire quot; هو الفوضى المنظمة (انهيار جليدي، بمعنى نظرية الكوارث la theacute;orie des catastrophes). إن وظيفة أو دالة موجة يؤثر على موجة تجريبية تصف مشهد التجاذبات الكسورية. إن هذه الظروف الخاصة التي يمكن تعديلها وفقا للموجة الموجهة هي حسب جاك سارفاتي أحد السبل الممكنة لتحقيق quot;رقائق الكمquot; quantum chips التي قال انه يقترح نظرية بشأنها على صفحاته وكتاباته وأبحاثه. ووفقا له، يمكن أن تنتج شركة أنتيل INTEL مثل هذه الرقائق في خمس سنوات من الاستثمار بمعدل مائة مليون دولار الدولار.
ذهب جاك سارفاتي إلى أبعد من ذلك، لأنه يقترح توسيع لنظرية بوم theacute;orie de Bohm والتي تمارس quot;مشاهد التجاذبات الكسوريةquot; بدورها،حسب ما ورد في النظرية، تأثير على برنامج الموجة القائدة أو الموجهة. يقترح جاك سارفاتي المعادلة التي يمكن أن نبسطها الى quot;موجة تجريبية = عامل يؤثر في وظيفة أو دالة موجة، وموجة موجهة، على غرار معادلة آينشتاينquot; بشأن العلاقة بين المادة والطاقة، إذ أن هذه الحلقة حسب جاك سارفاتي هي ميزة quot;للوعي الكوني حيث أن الموجة القائدة أو الموجهة، تعدل نفسها بنفسها s'automodifie لأنها تعي أو تدرك ذاتها!
يذهب جاك سارفاتي إلى أبعد من ذلك بافتراض أنه يوجد لها في هياكل الدماغ البشري بنى تسمى الأنابيب الدقيقة microtubules (التي يعرفها علماء البيولوجيا و يعرفون سلوكها الشاذ)، والتي هي في واقع الأمر quot;رقائق كمومية quantum chips quot;ركبت من الناحية البيولوجية. إن هذه الأنابيب الدقيقة هي السبب والأصل في وجود الوعي. إن هذه الأفكار ليست بعيدة عن تلك التي تحدث بها روجر بنروز Roger Penrose، وهو عالم رياضيات من صنف العباقرة، وعرضها في كتابه quot;الروح، والكمبيوتر، وقوانين الفيزياءquot; الذي نشر في فرنسا مترجماً عن الانجليزية، حيث يصل عبر طرق مختلفة لنفس النتيجة! وسنعرض نظريته لاحقاً.
نظرية جون بيير بتي الكونية La theacute;orie de lrsquo;univers de Jean-Pierre Petit
جون بيير بتي هو عالم الفلك الفرنسي الفذ والثائر الدائم أو المشاغب حسب وصف خصومه، الذي عمل في مرصد مرسيليا. نظريته الكونية، تتضمن العديد من العناصر المستلهمة من نظرية العالم الروسي أناتول ساخاروف Anatole Sakharov، الذي استمد جوهرها بدوره من نظرية الأوميين الكونية عن الكون التوأم والأكوان المتوازية، التي أرسلت له بالبريد كنصوص علمية فيزيائية مرسلة من مجهولين يزعمون أنهم كائنات فضائية جاءت من كوكب أومو وتشبه البشر خاصة سكان الشمال الأوروبي، ومع ذلك فإن نظرية جون بيير بتي نظرية أصيلة. وهي تتألف من جانبين:
bull; الجانب الأول يفسر لماذا لا نعرف أين هي المادة المضادة l'anti-matiegrave;re: حيث يفترض جون بيير بتي إنها موجودة في الكون التوأم غير المرئي الذي يتفاعل مع كوننا المرئي حيث يتجه سهم الزمان باتجاه معاكس والذي يسميه الكون الظل univers ombre.
bull; الجانب الثاني يتناول المفارقتين الكونيتين الأوليتين، و يقترح quot;نموذج القياس modegrave;le de jauge quot; للكون الذي لايكون فيه الانفجار الكبير ضرورياً... وبالمناسبة، فإن هذا النموذج يتيح لنا إمكانية الإبحار بسرعة تفوق سرعة الضوء!
ويمكن الاطلاع على هذه النظرية بالتفصيل في تقارير اكاديمية العلوم في باريس، المجلد 284، (مايو 23، 1977) سلسلة وحدة تخزين وAp1315 مجاد 284 حزيران6 يونيو 1977) ص 1413. حيث يعرض جون بيير بتي كذلك الفيزياء الهندسية physique geacute;omeacute;trique. وكذلك على صفحة جون بيير بتي على الانترنيت باللغتين الفرنسية والانجليزية.
الأكوان التوأم Les univers jumeaux
لنفترض وجود كونين، أو صفحتين كونيتين، تتألف كل منها من مجموعة من البلاطات carreaux كتلك التي تستخدم في الحمامات، ولكنهما ملتصقتين ببعضهما البعض، وفي لحظة الانفجار الكبير، تم فصل الطبقتين أو الصفحتين، ولكن في كل كون منهما تكون بعض البلاطات قد انتزعت بينما البعض الآخر ظلت ملتصقة مكونة سمكاً مضاعفاً sureacute;paisseur وفي كل واحد من هذين الكونين يمكن أن نعثر على البلاطات المزدوجة السمك التي سوف تركن للأماكن الحرة أو الفارغة، حتى لو كان الوضع متماثل تماماً parfaitement symeacute;trique. ولكن إذا حدث كسر في هذا التماثل أو التناظر، سيكون هناك وجود فائض من المادة في أحد الكونين، ووجود فائض من المادة المضادة في الكون ألأخر والتي لم تعد قادرة على ابادة إحداها للأخرى.
المادة والمادة المضادةet anti-matiegrave;re matiegrave;re
من البديهي أننا يمكن ننشيء، في أحد هذين الكونين، ولكن في المختبر، ومن تركيزات عالية جدا من الطاقة، لدرجة تسمح لنا بخلق زوجين من المادة و المادة المضادة. ولكن سرعان ما يجتمع جسيم المادة المضادة بجسيم للمادة، عند ذلك سيتم إبادة وإعدام بعضهما البعض. بحيث يظل مجموع المواد محفوظاً و سليماً.
الأمر الأصلي في النظرية هو أن الكونين التوأمين يمثلان متساويات أو تعادلات متعاكسة، اليمن في أحدها هو اليسار في الآخر، وسهام اتجاه الزمان متعاكسة في الكونين وإن مستقبل أحدهما هو ماضي الآخر!.
الكونين يتفاعلان عبر المجالات أو الحقول، مما يتسبب في حدوث حالات غريبة، مثل الجزيئات التي تبدو وهي تعبر الزمان (مثل هذه الجسيمات تظهر في نظرية quot;التكامل لفاينمان la theacute;orie des quot;inteacute;grales de Feynmann quot;: أنها دائما ما تكون quot;جسيمات افتراضيةquot;، أي أنها تقع في هذا الكون التوأم...
يتميز جون بيير بيتي عن زاخاروف Sakharov لأنه يرى أنه لا توجد فقط ورقة أو صفحة واحدة من الكون feuillet d'univers، الملصقة على نفسها على طول نوعا من شريط موبيوس ruban de moebius في ثلاثة أبعاد.
وهناك سهم واحد فقط من الزمان، وإن هذا الوهم بخصوص البنية التوأمية أو الهيكل التوأمي structure geacute;mellaire ينجم عن هندسة هذا الكون الخاصة جداً: وهناك أيضا نوع واحد فقط من المادة، أما المادة المضادة فهي ليست سوى مادة منظور إليها بالاتجاه المعاكس لسهم الزمان.
و إذا كانت هناك جسور بين الكونين (quot;الثقوب الدوديةquot; trous de vers) لوجدنا أنفسنا في الوقائع المتقهقرة reacute;trochroniens.
الآثار المترتبة على النظرية:
bull; إذاً هنا وبطبيعة الحال في حال تقبلنا هذا الافتراض فإننا سوف نلغي المفارقة الثالثة أو التناقض الثالث من خلال تقبل فكرة أن المادة المضادة تتواجد في الكون التوأم (أو في الجانب الآخر من كوننا)
bull; إن الطاقة الكلية للكون تبقى ثابتة: وهذا يزيل المفارقة الرابعة أو التناقض الرابع.
bull; وهذا يعطي تفسيرا أكثر وضوحا عن مصير الكون.
وفي كتابه الأخير: quot;لقد فقدنا نصف الكون on a perdu la moitieacute; de l'univers quot;، يقدم جون بيير بتي المزيد من التفاصيل حول نظرية الأكوان التوأم وخاصة ما يترتب عليها من نتائج رائعة (لأنها تتيح وغيرها لشرح بنية وديناميكية المجرات، وطبيعة عمل الكازارات quasars). كما يعطي أيضا بعض التجارب التي تمكننا اليوم من التحقق من صلاحية النظرية (مقياس لquot;ثابت هابل constante de hubble quot; في اتجاهات مختلفة وخصوصا في quot;أعماقquot; مختلفة (المسافات)، حيث سندرك أن هناك اختلافات تعزى للكون التوأم من quot;المادة المظلمة أو المعتمة matiegrave;re sombre quot;.
نموذج القياس للكون Modegrave;le de jauge de l'univers
يمكن أن نجد دراسة مفصلة لهذا النموذج في تفسير النموذج الكوني مع سرعة الضوء المتغيرة أو المتنوعة، في( JPP جون بيير بتي، رسائل الفيزياء الحديثة والمجلد 3 ص رقم 16 (1988) 1527-1532، والنموذج الكوني مع سرعة الضوء المتغيرة. تفسير التحولات الحمراء: JPP جون بيير بتي، رسائل الفيزياء الحديثة والمجلد. 3 رقم 18 (1988) ص 1733-1744
An interpretation of cosmological model with variable light velocity, J.P. Petit, Moderne physics letters A vol 3 ndeg;16 (1988) pp 1527-1532 et Cosmological model with variable light velocity. The interpretation of red shifts : J.P. Petit, Modern physics letters A vol. 3 ndeg;18 (1988) pp 1733-1744 وهي مجلة من المستوى الأعلى عالمياً..)
ولكي ننتهي من المفارقة الخامسة ينبغي للأجسام والمكونات في الكون أن تتوسع معه: والحال أنه يتم تحديد الحجم الهائل لهذه الأجسام والأجرام السماوية من قبل عدد معين من الثوابت:
bull; ثابت الثقالة أو الجاذبية G La constante de la gravitation
bull;ثابت بلانك La constante de Plank h
bull; bull; كتلة بروتون م La masse du proton m
bull; سرعة الضوء C La vitesse de la lumiegrave;re
ومن هنا السؤال: لماذا لا نقوم بتنويع وتعديل حجم هذه الثوابت؟ من الواضح، أنها تبدو ثابتة، ولكن ألا يمكن أن تختلف على امتداد مليارات السنين؟
أن الاعتراض العادي من علماء الفيزياء بشأن إمكانية أو عدم إمكانية المس بالثوابت الكونية أو الفيزيائية يتمثل بالتالي: يجب أن تكون سرعة الضوء ثابتة إذ أن هذا الثابت هو أحد ركائز أو دعامات نظرية النسبية!quot; ولكن ذلك وبكل بساطة غير صحيح دائماً في زمان ومكان من كوننا المرئي قد يصلح في نطاق نظام شمسي كنظامنا أو داخل مجرة واحدة من مجرات الكون المرئي الهائلة. ففي حقيقة الأمر، إن ما كتبه العملاق ألبرت آينشتاين هو أن ثابت آينشتين la constante d'Einstein يجب أن يظل ثابتاً وفق المعادلة الشهيرة، ولكن هذا لا يعني ثبات سرعة الضوء إذا تغير ثابت الثقالة أو الجاذبية G... أي أن هناك إمكانية لتصور سرعات متعددة للضوء حسب الظروف الكونية وتنوع باقي الثوابت الكونية.
هناك اعتراض كلاسيكي آخر: quot;- لو مسسنا بثوابت معينة في الفيزياء، فسوف يكون لذلك عواقب والتي من شأنها أن تتعارض مع هذه المشاهدات ونتائج الرصد والمراقبة.quot; نعم، ولكن ماذا لو قمنا بتعديلها كلها في وقت واحد؟
لنبدأ من افتراض معقول يتعلق بإحدى المسلمات الفيزيائية ألا وهو: الحفاظ على الطاقة: أو قانون حفظ الطاقة. أنه يعطي نتائج مثيرة للاهتمام لأنها تمكننا من العثور على القوانين وعلى أشكال مختلفة من الثوابت الفيزيائية وقوانين القياس Lois de jauge. (وسوف نرى المعادلات المتعلقة بذلك فيما بعد).
إذاً يتم حفظ الطاقة، ولكن ليس الكتلة، والأشياء أو الأجسام والمكونات في الكون تتسع معه، كل الأشياء والأجسام والأجرام والمكونات، وهذا يعني الفوتونات والمجرات والثقوب السوداء والكواكب والذرات، أنت وأنا وكل شيء... لماذا لا يوجد من يدرك ذلك؟ لنقم بتجربة تفكيرية: لنعلن فجأة أن quot;الكون قد تضاعف فقط في حجمهquot;: عندها لا يمكن لأحد أن يلاحظ أو يدرك ذلك، لأن القواعد التي نتوسلها في إجراء القياسات توسعت بدورها معه! (جميع quot; القواعدquot; من جميع الأنواع، حتى قياس المسافة التي يقطعها الضوء في هذه المدة من الزمان) وبالتالي فإن سرعة الضوء، التي كانت لا نهائية في لحظة الانفجار الكبير، سوف تنخفض مع التوسع: فالكون البدائي سيكون تصادمي collisionnel، لأن سرعة الضوء ستكون مرتفعا جدا، (من الناحية التقنية نحن نقول أن آفاق الجسيمات تنمو بنفس سرعة تنامي نصف قطر الكون): وبالتالي يختفي التناقض الثاني أو المفارقة الثانية.
الكتل تتزايد، ولكن الطاقة تبقى ثابتة MC2.
وماذا عن الانزياح نحو الأحمر؟ سوف نجد أن ثابت الزمان la constante de temps يختلف مثل T: لذلك عندما يصل فوتون ذو طاقة hv منبعثة في فترة زمنية قريبة من الانفجار الكبير إلى الأرض، ويكون هذا الفوتون محتفظاً بنفس القدر من الطاقة، فإننا سوف نقيس تردد v أقل أو اضعف بسبب زيادة h، وبالتالي فإن الانزياح نحو الأحمر لا يعود أو يعزى الى الانفجار الكبير لأنه لم يكن قد حدث انفجار كبير! إن وتيرة انزلاق تردد dv يتناسب مع المسافة مع المصدر: حيث سنجد هنا قانون هبل la loi de Hubble!
إذن هل الكون في حالة توسع أم لا؟ السؤال ليس له معنى! ما يهم هو العثور على ما هو قابل للمشاهدة والرصد، أي ألـ red shift. عندها نحن لا نستطيع قياس أي توسع لأن القواعد تتوسع جنبا إلى جنب مع الكون وفي نفس الوقت... وبالمثل، فإنه من المستحيل قياس التغيرات في h, c, G، الخ... لأن أجهزة القياس quot;تنحرفquot; في نفس الوقت وبالتوازي.
وماذا عن الأنثروبي هل يتزايد مع الزمان t؟ سنرى أن التناقض الأول أو المفارقة الأولى تسقط
ولكن ماذا عن الفرادة الأولى الشهيرة t=0، إذا كان لنا أن نبادل المتغير الزماني variable chronologique المرموز له بـ t مقابل الأنثروبي S فإن الفرادة لن تعد موجودة، وذلك لأن هذه الحالة الأولية أو البدئية ستتوافق مع S = -oo. من هنا أيضاً تعتبر مسألة حالة الكون قبل الانفجار الكبير ليس لها معنى. فالزمان لن يكون المتغير الجيد لوصف الأحداث: وبالاستعاضة بالأنثروبي عن الكون، فإن هذا الأخير يصبح خط مستو conformeacute;ment plat.
وبخصوص زمن بلانك temps de planck، والذي هو الجذر التربيعي لـ (hG/c5)، نجد أنه يتنوع... وبالتالي مثل t! فإن حاجز أو جدار بلانك سيختفي...كما في الرسم البياني التالي:
نظرية لوران نوتال La theacute;orie de Laurent Nottale
لوران نوتال Laurent Nottale هو فيزيائي في المركز القومي للبحوث العلمية في فرنسا CNRS، ويعمل في مرصد مودون l'observatoire de Meudon.
نظريته هي امتداد لنظرية النسبية، والنسبية الجدولية relativiteacute; d'eacute;chelle والنسبية الكسورية relativiteacute; fractale،. وهي نظرية مثيرة للاهتمام لأكثر من سبب، لأنها تسمح للاستدلال على ميكانيكا الكم بالنسبية! أو بتعبير أدق تتيح انسياب الميكانيك الكمي من النسبية.
والمقصود هنا نظرية كسورية theacute;orie fractale وليس تمييزية من الزمكان. فلأول مرة في تاريخ العلم، اكتشفت لورن نوتال L Nottale المعادلات غير المتطابقة في ظل انعكاس الزمان. وبالتالي فإن نظرية النسبية المقياسية la relativiteacute; d'eacute;chelle تؤدي إلى عدد كبير جدا من التوقعات، والتي يبدو بعضها quot;غريبة جداًquot; (على سبيل المثال كمومية مسافات الكواكب من نجومها) والتي تم التحقق منها بعد التجربة!
ومع ذلك هناك منتقدين كثر لهذه النظرية الذين يتهمونها من بين أمور أخرى باحتوائها على عدد كبير من الافتراضات الـ المناسبة أو الموائمةquot; ad-hoc المرتبة وفق الحاجةquot;
كوزموس الرياضيات! Cosmo Maths
يبقى هناك تساؤل بشأن معرفة ما كان يجري خلال الانفجار الكبير: كيف بنت هيكليات الكون نفسها أو كيف تشكلت؟ أي كيف ولدت تلك البنيات والهيكليات الكونية؟ سوف نرى أن الجواب، وهو ليس بديهياً، على هذا السؤال البسيط سوف يعطينا بعض المفاتيح لاختيار النظرية الصحيحة.
العلم الحديث لديه سمعة بناء نفسه من حسابات معقدة فظيعة بحث لايفهمها سوى الرؤوس الكبيرة أو العباقرة. لكن الأفكار الأساسية هي بسيطة دائما، وأنه من الشائع أنها يمكن أن تكون وسيلة صالحة تماما لتبرير استخدام الحسابات التي تشبه حسابات البقال.
الملاحظات أدناه أمثلة مستمدة من حسابات جون بيير بتي التي يمكن تطبيقها على باقي النظريات.
كيفية العثور على قوانين تطور الكون في ثلاثة خطوط من العمليات الحسابية
لنشبه الكون بكتلة grumeau متجانسة من الغبار من دائرة نصف قطرها R والكتلة M. ولنعتبر جسيم الغبار من كتلة m تقع على سطحه. كان نيوتن قد أظهر أن القوة التي تمارس على هذه الكتلة هي نفسها تلك التي تنتجها أية كتلة M تتركز في مركز O، أي:
F = - GMm / R2
لنطبق معادلة F = my من ميكانيكا الكم، وبسبب صعوبة كتابة الحروف الإغريقية سنلجأ إلى مفردات معادلة فريدمان -mRquot; = GMm/R2ou : R2 Rquot; + GM =0 لنفعٌل واحد من ثلاث حلول لهذه المعادلة التمييزية وتحديد إثنين من الثوابت ونعطي لـ R(t) شكل a tb و b فنضعها في المعادلة R = a tb =gt; R' = ab tb-1 =gt; Rquot; = ab(b-1) tb-2
فسوف نحصل على b(b-1)a3t3b-2 + GM = 0
R = a tb =gt; R' = ab tb-1 =gt; Rquot; = ab(b-1) tb-2. b(b-1)a3t3b-2 + GM = 0
والتي يجب أن تعمل مهما كانت قيمة t. والحل الوحيد هو أن هذه الأخيرة تساوي لا شيء nu إذن b = 2/3 فيعطينا ذلك a = sqrt(9/2 GM) et
R = racinecubique(9/2 GM t2/3).
R(t) هو الطول التمييزي لهذا الكون والذي يمكن مقارنته بنصف قطر تحدبه أو بمتوسط المسافة بين جسيمين أو جزيئين فيه.
الكون الانطوائي L'univers autistique
وتكشف نظرة سريعة على المنحنى أو الرسم البياني أدناه بأن R(t) يدل على ان توسع الكون بدأ بانفجار، وإن معدل التوسع صار يتباطأ بعد ذلك. ولو نسبناR(t) إلى متوسط المسافة بين اثنين من الجزيئات، فإن ct يمثل نصف قطر دائرة من الموجات الكهرومغناطيسية التي تنبعث في الزمن t = 0. مع سرعة ضوء ثابتة، سوف نرى بأن نصف قطر هذه الكرة الأفق sphegrave;re horizon، هو مجال من معرفته نجد أنه يبقى لفترة من الزمن أقل من متوسط المسافة بين الجسيمات، والتي سوف تتجاهل تماما خلال هذه الفترة.
لهذا السبب لم يكن الكون المرئي البدائي تصادمياً collisionnel
كيفية حساب قطر الثقب الأسود Comment calculer le rayon d'un trou noir
الثقب الأسود هو في الأصل نجم من دائرة نصف قطرها R وكتلة M على سطحه. والآن لنفترض أنه صاروخ. فإن مقدار الطاقة التي سيستغلها لا تتجاوز MC2، والذي يمثل الطاقة المعادلة. لحساب الطاقة المستهلكة لاستخراج هذه الكتلة من مجال الثقالة الجاذبية للنجم: فإن القوة هي F = -GMm/r2، والفعل هو GMm/r2 dr، حيث يمثل dr زيادة في نصف قطر دائرة. و إن الطاقة هي التي أعطت الرمزE وهو المجموع الكلي لـ R في اللانهاية من الفعل، أي E = GMm / R
وهذه الطاقة تفوق الطاقة القصوى المتاحة إذا كان GMm/R gt; mc2,، حيث:
R lt; GM/c2 (Rayon de Schwartzchild) وهو المعروف بنصف قطر شوارزشيلد.
في الواقع، إذا قمنا بعملية حسابية أكثر دقة مع الأخذ في الاعتبار الانخفاض في الكتلة فإن ذلك سيقودنا إلى Rs = 2GM/c2
إذا كانت هناك كتلة M مستمرة داخل دائرة نصف قطرها شوارزشيلد، فلا يمكن لأي جسم الخروج لأن الطاقة الضرورية اللازمة لعملية الخروج يجب أن تكون أكبر من MC2. والحال أن نصف قطر شوارزشيلد للشمس هو 3.7 كم.
وماذا عن الفوتون؟ للفوتون طاقة hv وهي تمثل كمية معادلة من المادة m = hv/c2 التي من خلالها يمكن للمرء أن يحسب الطاقة اللازمة للاستخراج:
- مجموع R في اللانهاية من GMm / r2 dr = GMhv / Rc2. ما يعني أن طاقة فوتون نجح في مغادرة النجم تحسب وفق المعادلة E' = hv(1- GM/Rc2 التي هي أقل من hv أي ظاهرة ريد شيفت الثقالية pheacute;nomegrave;ne de red shift gravitationnel). لذا إذا كان R lt; GM/c2 لنجم لا يمكنه أن يبعث الضوء: فهو إذاً ثقب أسود.
شروط بلانك Les conditions de Planck
إن البعد المكاني لجسيم (حجمه) يعطى من خلال الطول الموجي للكومبتون Compton
Lc = h / mc. (نلاحظ أنه كلما كان الجسيم ثقيل، كلما كان حجمه صغيراً) لنفترض أن هذا الجسيم هو عبارة عن ثقب أسود: إذن فإن هذا الطول Lc يجب أن يكون مساويا لنصف القطرشوارزشيلد rayon de schwartzchild, أي h/mc = GM/c2، مما يعطينا المعادلة mp=. التي تعادل 10^-5 grammes غرام، وهذه هي كتلة بلانك masse de Planck. ولا يمكن أن يكون هناك جسيم أثقل من ذلك. حيث تعطى نصف قطر هذه الكتلة بواسطة طول كومبتون لها وفق المعادلة = Lp وهذا هو طول بلانك الذي يعادل 1,6 10^-33 cm سم ولا يمكن أن يوجد ما هو أصغر من ذلك في الكون: quot;وهي المعروفة بالخلية الأولية للمكان maille eacute;leacute;mentaire de l'espace.
وهذا يعني أن الفوتون يبلغ طوله الموجي L = c/v حيث V هو تردده وطاقته هي E= hc / L أي كتلته المعادلة هي mphoton = E/c2 = h / (L c) و نصف قطر شوارزشيلد فيه schwartzchild هو Rs = Gmphoton / c2 = Gh / Lc3 الذي يعادل طول الموجة إذا كان = Lp L = عندما يكون طول الموجة يساوي نصف قطر شوارزشيلد فسوف يدور حول نفسه مثل الثعبان الذي يحاول عض ذنبه ولا يمكن للمعلومة أن تنتشر.ويضاف لهذا الطول الموجي الزمن كما في المعادلة Tp = Lp / c = 0,54 10^-43 secondes ثانية وهو ما يعرف بزمن بلانك le temps de Planck أو سُمك الحاضر.
نظرية النسبية الفائقة لجون بييربتي La super-relativiteacute; ou la theacute;orie de jean-pierre Petit
لنحرركل quot;الثوابتquot; في الفيزياء من قيمها المتعارف عليها ونطلق سراحها. على سبيل المثال G، ثابت الثقالة أو الجاذبية و h ثابت بلانك و c ثابت سرعة الضوء و m كتلة البروتون أو النيوترون.
في معادلة اينشتاين النسبية العامة، نعرف أن الثابت هو ثابت ذو قيمة مطلقة التي فرضها الهيكل الرباعي الأبعاد للكون وفي هذه الحالة فإن G ~ c2، ولنفترض أنه يتم حفظ الطاقة وفق صيغة mc2 على مر الزمن، حيث أن m هو كتلة الجسيم في حالة سكون.
ولنفترض أيضاً أن المجرات، و النظام الشمسي، والثقوب السوداء، والبروتونات والنيوترونات quot;كلها تنموquot; جنبا إلى جنب وفي نفس الوقت مع الكون، والذي يكون المحيط peacute;rimegrave;tre يساوي 2pi R ولنفترض أن نصف قطر شوارزشيلد rayon de schwartzchild لثقب أسود ينمو كـ R : Gm/c2 ~ R وكـ G/c2 =constante أي يساوي = ثابت، فسوف نحصل على m ~ R. مثلما هو الحال مع , Rc2 = constante و mc2 = constante وهذا هو قانون تنوع سرعة الضوء حيث يمكن أن نستنتج من ذلك أن G ~ 1/R.
لنأخذ الآن نجمتين بنفس الكتلة أو بكتلة متساوية m تدور حول بعضها البعض أو حول مركز الثقل المشترك بينهما في مسار دائري نصف قطره r فإن قوة الطرد المركزي هي mv2/R حيث V هي سرعة)، و حيث أن الثقالة أو الجاذبية المتبادلة هي Gm2 / 4r2. وإذا تنوع r مثل R (وهذا الأخير R هو نصف قطر الكون)، عندها ستكون Gm2/R2 ~ mv2/R.من هنا تأتي V ~ R-1/2 حيث يتم الحفاظ على صيغة بيتا = betaquot; = v/c مع مرور الزمن مثلما يتم الحفاظ على صيغة الطاقة تساوي E =، حيث الطاقة E تتعامل مع التمديد المكاني للبروتون بواسطة طول موجة كومبتون onde de Compton وفق الصيغة التالية h/mc ~ R, on a h ~ R3/2.
وهنا يأتي حل معادلة آينشتاين، على افتراض أن الكون متجانس وموحد الخواص l'univers homogegrave;ne et isotrope ( قياس روبرتسون، وولكر meacute;trique de Robertson-Walker) فإن ذلك سيؤدي إلى المعادلة التفاضلية التالية: 2Rquot;/R + R'2/R2 (2+beacute;ta2) + kc2 (1+ beta2) / R2 = 0 , avec (beta = v/c)
حيث V = beta بيتا. و c هي سرعة الإثارة أو الاضطراب للمجرات في هذا quot;السائل الكونيquot;. وفي البحث عن حل من نوع R = a tb سنلاحظ أن بيتا ستلغي نفسها وإن الحل الوحيد الممكن هو مع k وإن k هو quot;مؤشر انحناءquot;، وبالتالي فإن الكون لديه انحناء سلبي. وإن حل المعادلة سيكون R ~ t2/3. وهذا هو تنوع نصف قطر الكون على مر الزمن.
ويعرف الأفق الكوني من خلال مجموع تام H يساوي، من صفر إلى زمن غير محدد، وفق الصيغة الرياضية التالية : H = somme de 0 agrave; t de c(t)dt إذ نعثر على معادلة H = R(t)
و يصبح الأنثروبي S ~ Log t. في وصف يحل فيه الأنثروبي محل متغير الزمن la variable temps، حيث تختفي الفرادة البدئية أو التأسيسية الأولية singulariteacute; initiale كما يبين الرسم البياني التالي:
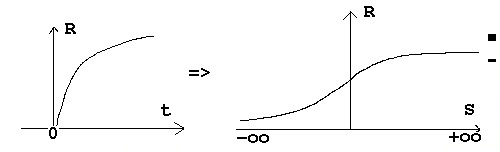
يمكن للمرء أن يتساءل أيضا عما إذا كان من الممكن العثور على بدائل مشابهة للمتغيرات بشأن المكان espace. كما نلاحظ من ذلك أن كل المعادلات في الفيزياء (بولتزمان، شرودنغر، ماكسويل boltzmann, schrouml;dinger, Maxwell) هي ثابتة في ظل التحولات التي حصلنا عليها. وعلاوة على ذلك نجد أن التحول للأحمر red shift يتناسب مع المسافة (قانون هابل loi de Hubble).
ــــــــــــــــــــــــــــــــــــــــــــ
كل المعادلات والرسوم البيانية في هذه الدراسة هي للعالم الفرنسي جون بيير بتي وبرخصة منه.







التعليقات